Mineral Potential Mapping using Geochemistry Data
Exploration of Statistical Methods to Assess Stream Sediment and Soil Sampling Results
Latar Belakang
Proyek ini merupakan soal UAS Geokimia Eksplorasi, di mana diberikan 2 dataset: [Soil Sample Data, Stream Sediment Data]. Perlu diketahui bahwa dalam eksplorasi Cu-Au, Stream Sediment Sampling (SSS) dilakukan terlebih dahulu, baru kemudian Soil Sampling (SS) akan dilakukan pada area yang lebih berpotensi yang diketahui dari SSS. Ujian ini memberikan 2 tugas utama: Lakukan klasterisasi data (minimal 3 klaster), Buat Peta Anomali Tiap unsur.
Metode
Klasterisasi akan menggunakan pendekatan principal component analysis (PCA) dan k-means clustering (KMC) sedangkan peta anomali akan menggunakan aplikasi surfer untuk menginterpolasi data.
Output
1. Klasterisasi
A. Deskripsi Data
1
2
3
4
5
6
7
8
9
10
# import library
import numpy as np
import scipy as sc
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
# import dataset
soil = pd.read_csv("soil.csv", delimiter=',')
stream = pd.read_csv("stream.csv", delimiter=';')
1
2
# deskripsi data stream sediment sampling
print(stream.describe())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
Northing Easting Elevation Au Ag \
count 1.130000e+02 113.000000 113.000000 113.000000 113.000000
mean 9.795687e+06 749714.548673 1229.380531 0.004376 0.069027
std 1.023627e+03 839.607572 40.986348 0.003059 0.042426
min 9.794083e+06 748207.000000 1146.000000 0.002500 0.050000
25% 9.794859e+06 749068.000000 1199.000000 0.002500 0.050000
50% 9.795451e+06 749692.000000 1224.000000 0.002500 0.050000
75% 9.796515e+06 750225.000000 1257.000000 0.006000 0.100000
max 9.798096e+06 751401.000000 1346.000000 0.017000 0.400000
As Cu Mo Pb Sb Zn
count 113.000000 113.000000 113.000000 113.000000 113.000000 113.000000
mean 6.353982 29.716814 1.340708 15.176991 0.929204 62.991150
std 5.990946 19.983238 1.498907 11.950217 0.485813 36.442346
min 1.000000 7.000000 0.500000 4.000000 0.500000 27.000000
25% 3.000000 21.000000 0.500000 10.000000 0.500000 46.000000
50% 4.000000 26.000000 1.000000 13.000000 1.000000 58.000000
75% 8.000000 33.000000 1.000000 18.000000 1.000000 73.000000
max 32.000000 146.000000 10.000000 109.000000 3.000000 383.000000
1
2
# deskripsi data soil sampling
print(soil.describe())
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
Northing Easting Elevation Depth Au \
count 2.420000e+02 242.000000 242.000000 242.000000 242.000000
mean 9.795762e+06 749275.483471 1294.037190 84.359504 0.012308
std 1.041078e+02 274.960642 31.628462 13.173865 0.035687
min 9.795471e+06 748698.000000 1231.000000 50.000000 0.002500
25% 9.795710e+06 749056.500000 1264.000000 80.000000 0.002500
50% 9.795777e+06 749285.000000 1303.500000 85.000000 0.006000
75% 9.795826e+06 749530.500000 1321.000000 90.000000 0.008750
max 9.795991e+06 749737.000000 1345.000000 140.000000 0.460000
Ag As Cu Mo Pb Sb \
count 242.000000 242.000000 242.000000 242.000000 242.000000 242.000000
mean 0.243182 17.847107 27.355372 0.900826 14.231405 1.324380
std 0.131875 30.253105 13.115421 0.415568 5.971246 4.169035
min 0.050000 1.000000 2.000000 0.500000 3.000000 0.500000
25% 0.100000 5.000000 20.000000 0.500000 10.000000 0.500000
50% 0.300000 7.000000 29.000000 1.000000 13.000000 0.500000
75% 0.300000 14.000000 34.000000 1.000000 16.750000 0.500000
max 0.700000 244.000000 114.000000 4.000000 52.000000 49.000000
Zn
count 242.000000
mean 65.305785
std 23.104074
min 4.000000
25% 52.000000
50% 71.000000
75% 81.000000
max 118.000000
1
2
3
4
# Sebaran spasial data SSS
sns.scatterplot(x = stream['Easting'], y = stream['Northing']).set(title='Sebaran data Stream Sediment Sample')
plt.show()
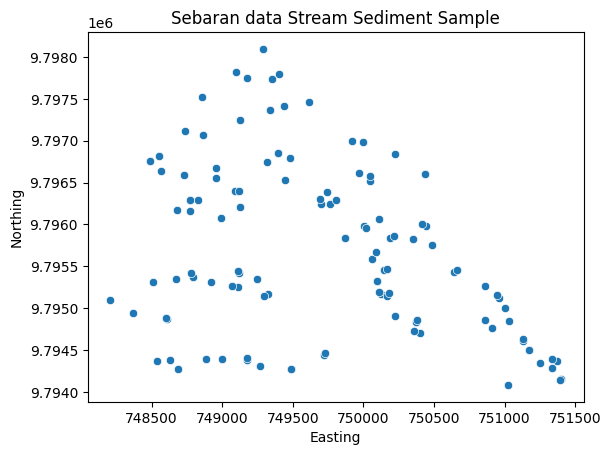Sebaran data Stream Sediment Sampling.
1
2
3
# Sebaran spasial data SS
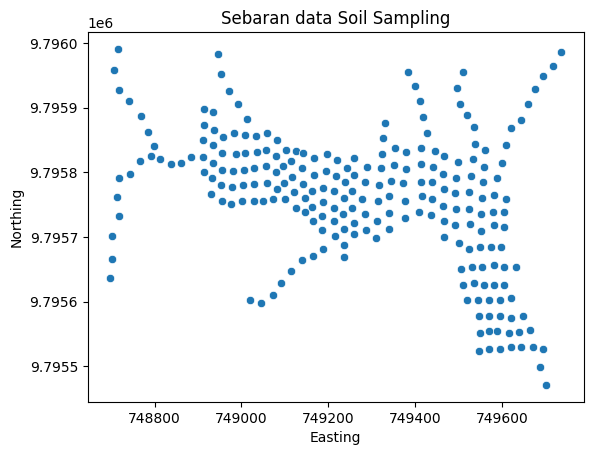
sns.scatterplot(x = soil['Easting'], y = soil['Northing']).set(title='Sebaran data Soil Sampling')
plt.show()
Sebaran data Soil Sampling.
1
2
3
4
# ambil parameter koordinat
coordinates = ["Northing", "Easting"]
costream = stream[coordinates]
cosoil = soil[coordinates]
1
2
3
4
5
6
# korelasi antar unsur SSS
streamm = ["Au", "Ag", "As", "Cu", "Mo", "Pb", "Sb", "Zn"]
streamn = stream[streamm]
heatmap = sns.heatmap(streamn.corr(), cmap="YlGnBu", annot=True)
plt.show()
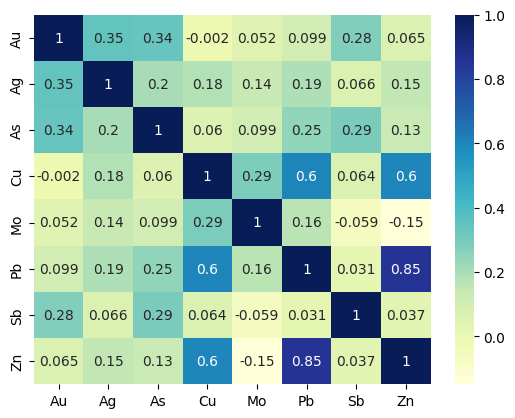Heatmap Stream Sediment Sampling.
1
2
3
4
5
6
# korelasi antar unsur SS
soilm = ["Au", "Ag", "As", "Cu", "Mo", "Pb", "Sb", "Zn"]
soiln = soil[soilm]
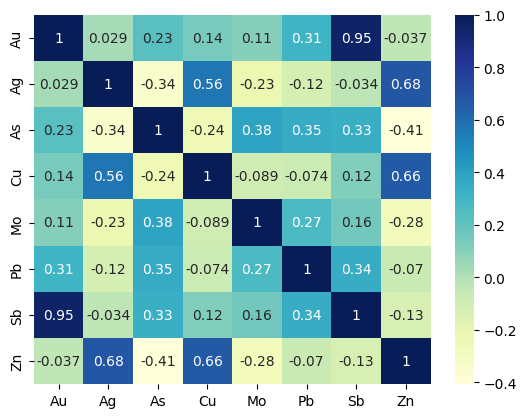
heatmap = sns.heatmap(soiln.corr(), cmap="YlGnBu", annot=True)
plt.show()
Heatmap Soil Sampling.
B. Principal Component Analysis
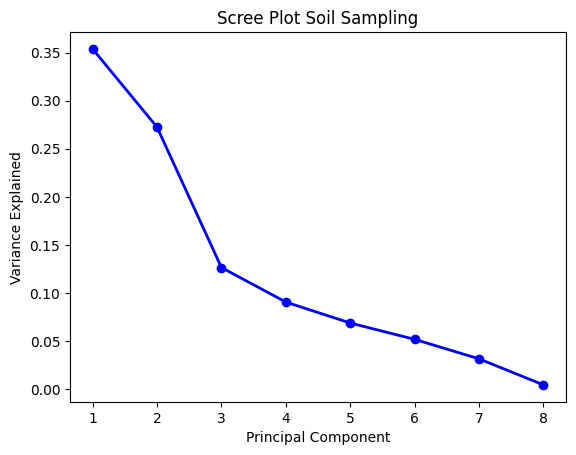
Pada proses ini, akan dilakukan reduksi dimensi, sehingga hanya terdapat beberapa parameter yang memiliki explained variance >70%. Dalam hal ini, data SSS membutuhkan 4 principal component (PC), sedangkan data SS membutuhkan 3 PC saja.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
from sklearn.preprocessing import RobustScaler
from sklearn.preprocessing import PowerTransformer
from sklearn.preprocessing import QuantileTransformer
from sklearn.preprocessing import StandardScaler
from sklearn.decomposition import PCA
# Stream Sediment Sampling
# Standarisasi
sss = StandardScaler().fit_transform(streamn)
# fitting
pcasss = PCA(n_components=8)
componentsss = pcasss.fit_transform(sss)
PC_valuesss = np.arange(pcasss.n_components_) + 1
plt.plot(PC_valuesss,
pcasss.explained_variance_ratio_,
'o-',
linewidth=2,
color='blue')
plt.title('Scree Plot Stream Sediment Sampling')
plt.xticks([1, 2, 3, 4, 5, 6, 7, 8])
plt.xlabel('Principal Component')
plt.ylabel('Variance Explained')
plt.show()
# PCA Components
print("PCA Komponen: \n", abs(pcasss.components_))
explained_variance = pcasss.explained_variance_ratio_
print("explained variance: \n", explained_variance)
loadingsss = pcasss.components_.T * np.sqrt(pcasss.explained_variance_)
print("loadings: \n", loadingsss)
# mengambil 3 komponen saja
pcas = PCA(n_components=3)
componentsss = pcas.fit_transform(sss)
data_pca_sss = pd.DataFrame(data=componentsss, columns=['PC1', 'PC2', 'PC3'])
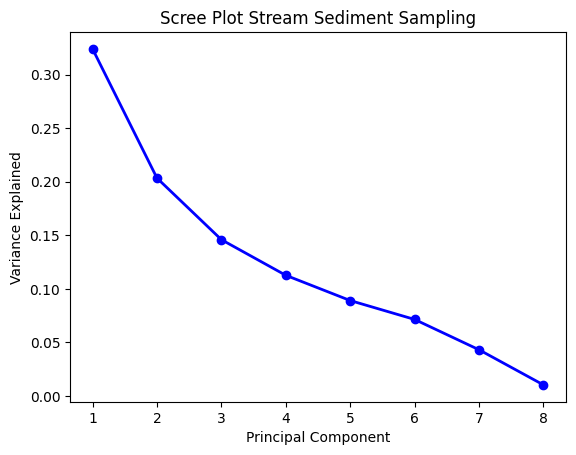Screeplot PC Stream Sediment Sampling.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
PCA Komponen:
[[0.19187024 0.25994356 0.25220231 0.472332 0.1332234 0.5540761
0.12770889 0.51754543]
[0.56300724 0.31584221 0.45953616 0.24962305 0.04131893 0.20264922
0.44275346 0.26641472]
[0.00956807 0.27145768 0.06124515 0.17747241 0.82339094 0.06851128
0.32117508 0.32427131]
[0.26388953 0.64159068 0.25996068 0.17254489 0.35499856 0.025459
0.53082358 0.11369527]
[0.03795414 0.2514599 0.69461527 0.31345984 0.00985173 0.1748355
0.56784124 0.03836362]
[0.74734345 0.5247963 0.32561651 0.01394463 0.12862289 0.08915249
0.17360899 0.07220768]
[0.12712045 0.09315561 0.24927682 0.73231464 0.29891363 0.4569437
0.22384632 0.16877401]
[0.01889618 0.00489485 0.05687332 0.13633179 0.26562641 0.63188436
0.00646296 0.71268579]]
explained variance:
[0.32406392 0.20344352 0.14592823 0.11265931 0.08907845 0.0714307
0.04310626 0.01028961]
loadings:
[[ 0.31031171 -0.72145811 -0.01038411 0.25164071 -0.03218257 -0.56746345
0.07498265 0.00544564]
[ 0.42040669 -0.40473179 0.29460966 0.61181031 -0.21322115 0.39848174
-0.05494832 0.00141063]
[ 0.40788675 -0.58886648 -0.0664686 -0.24789422 0.5889872 0.24724304
0.14703722 -0.01639016]
[ 0.76390247 0.31987612 0.19260861 -0.16453597 -0.26579294 0.01058826
0.43195956 0.03928907]
[ 0.21546218 -0.05294759 0.89361602 -0.33852078 0.00835361 -0.09766432
-0.17631574 -0.07655011]
[ 0.89610719 0.25968213 -0.07435445 -0.02427728 0.14824879 -0.06769415
-0.2695306 0.18210094]
[ 0.20654356 -0.56736051 -0.34856735 -0.50618462 -0.48149132 0.1318226
-0.13203691 -0.00186254]
[ 0.83702615 0.34139359 -0.35192765 0.10841794 0.03252978 -0.05482783
-0.09955222 -0.20538687]]
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
# Stream Sediment Sampling
# Standarisasi
ss = StandardScaler().fit_transform(soiln)
# fitting tes
pcass = PCA(n_components=8)
componentss = pcass.fit_transform(ss)
PC_valuess = np.arange(pcass.n_components_) + 1
plt.plot(PC_valuess,
pcass.explained_variance_ratio_,
'o-',
linewidth=2,
color='blue')
plt.title('Scree Plot Soil Sampling')
plt.xticks([1, 2, 3, 4, 5, 6, 7, 8])
plt.xlabel('Principal Component')
plt.ylabel('Variance Explained')
plt.show()
# PCA Components
print("PCA Komponen: \n", abs(pcass.components_))
explained_variance = pcass.explained_variance_ratio_
print("explained variance: \n", explained_variance)
loadingss = pcass.components_.T * np.sqrt(pcass.explained_variance_)
print("loadings: \n", loadingss)
# mengambil 3 komponen saja
pc = PCA(n_components=3)
componentss = pc.fit_transform(ss)
data_pca_ss = pd.DataFrame(data=componentss, columns=['PC1', 'PC2', 'PC3'])
Screeplot PC Soil Sampling.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
PCA Komponen:
[[0.25717541 0.40782702 0.42716077 0.33200723 0.30768537 0.28362766
0.30967742 0.45147288]
[0.54750278 0.32132918 0.05043709 0.40949871 0.02680319 0.24001289
0.5279991 0.29941197]
[0.34377274 0.16093001 0.27196637 0.24301009 0.64432738 0.40730594
0.30165204 0.22550472]
[0.09265709 0.00498547 0.04540232 0.25393928 0.53050676 0.78047057
0.11132689 0.1479117 ]
[0.12641922 0.14527307 0.85096514 0.12075254 0.41069418 0.22270364
0.04541753 0.06214266]
[0.06567812 0.76093541 0.02986977 0.61669095 0.14820255 0.06481802
0.01970675 0.09439298]
[0.16079029 0.32301269 0.10127755 0.44556875 0.1316913 0.18094617
0.00192298 0.78162192]
[0.67910789 0.00609871 0.06059449 0.07157191 0.00630966 0.01941447
0.72074574 0.10044847]]
explained variance:
[0.35372096 0.27247903 0.12651242 0.09061089 0.06881786 0.05182689
0.03156874 0.00446321]
loadings:
[[ 0.43351486 0.81002239 0.34656298 -0.07905203 -0.09399567 -0.04237819
-0.08097157 -0.12858986]
[-0.68746494 0.47540184 -0.1622362 -0.00425344 0.10801395 -0.49098647
0.16266434 -0.0011548 ]
[ 0.7200554 0.07462094 -0.27417378 -0.03873579 0.63271264 -0.01927319
-0.05100186 -0.01147364]
[-0.5596572 0.60584738 -0.24498248 -0.21665276 0.08978236 0.39791408
0.22438173 -0.01355222]
[ 0.51865838 0.03965493 -0.64955707 -0.45261118 -0.3053608 -0.09562631
-0.06631776 0.00119474]
[ 0.47810483 0.35509558 -0.41061184 0.6658722 -0.1655854 0.04182322
0.09112178 -0.00367615]
[ 0.52201633 0.78116698 0.3041004 -0.0949805 -0.033769 -0.0127156
0.00096838 0.13647404]
[-0.76103779 0.44297565 -0.22733504 0.12619347 0.04620453 0.06090619
-0.39361306 0.01902003]]
C. K-Means Clustering
Data akan dibagi menjadi beberapa klaster (minimal 3) menggunakan algoritma KMC
Berdasarkan nilai silhouette score terbesar, data SSS memiliki jumlah klaster ideal 4, sedangkan data SS sejumlah 5.
1. Memeriksa Jumlah Klaster ideal
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
from sklearn.cluster import KMeans
from sklearn.metrics import silhouette_score
from sklearn.pipeline import Pipeline
def silKMC(df, nama):
x = df.iloc[:, 0:8].values
sc = []
K = range(3, 20)
for k in K:
# Building and fitting the model
# membuat pipeline untuk preprocessor
preprocessor = Pipeline([("scaler", RobustScaler()),
("pca", PCA(n_components=3,
random_state=None))])
# membuat pipeline untuk clusterer
clusterer = Pipeline([("KMC",
KMeans(n_clusters=k,
init="k-means++",
n_init=50,
max_iter=500,
random_state=42))])
# membuat pipeline untuk fitting
pipe = Pipeline([("preprocessor", preprocessor),
("clusterer", clusterer)])
# Data Lengkap
pipe.fit_predict(x)
pra = pipe["preprocessor"].transform(x)
pasca = pipe.fit_predict(x)
score = silhouette_score(pra, pasca, metric="euclidean")
sc.append(score)
figx, ax = plt.subplots()
plt.plot(K, sc)
plt.xticks(np.arange(3, 21, 1.0))
plt.xlabel('Jumlah Klaster')
plt.ylabel('Silhouette Score')
plt.title(f"Silhouette Score K-Means Clustering {nama}")
plt.show()
silKMC(streamn, "Stream Sediment Sampling")
silKMC(soiln, "Soil Sampling")
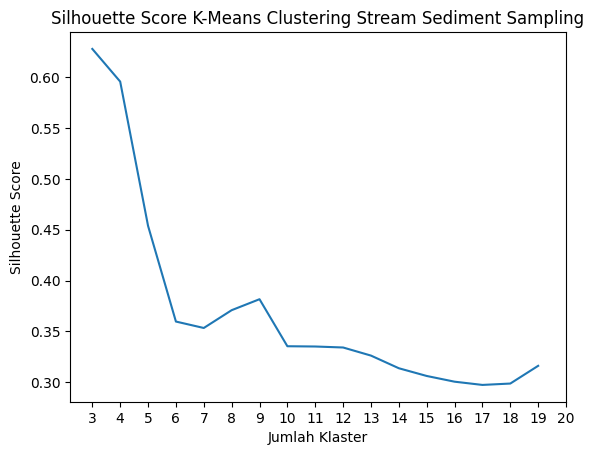Screeplot Silhouette Score Stream Sediment Sampling.
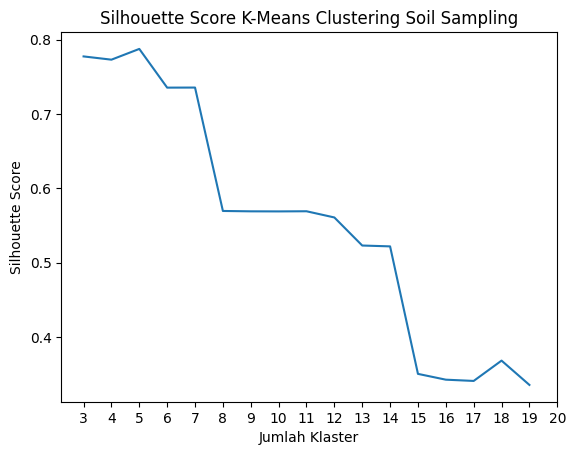Screeplot Silhouette Score Soil Sampling.
2. K-Means Clustering
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
def kmc(nama, df, parameter, loadings, data_pca, jumlah_klaster, coor):
x = df.iloc[:, 0:8].values
# Membuat pipeline untuk preprocessor
preprocessor = Pipeline([("scaler", RobustScaler()),
("pca", PCA(n_components=3, random_state=None))])
# Membuat pipeline untuk clusterer
clusterer = Pipeline([("kmeans",
KMeans(n_clusters=jumlah_klaster,
init="k-means++",
n_init=50,
max_iter=500,
random_state=42))])
# Membuat pipeline untuk fitting
pipe = Pipeline([("preprocessor", preprocessor), ("clusterer", clusterer)])
# Melukukan prediksi terhadap Dataset
pipe.fit(x)
pipe.predict(x)
pra = pipe["preprocessor"].transform(x)
pasca = pipe["clusterer"]["kmeans"].labels_
# silhouette_score
score = silhouette_score(pra, pasca, metric="euclidean")
print(f'silhouette score KMC: {score}')
# Tambah data pada datafrane PCA
pcadf = data_pca
pcadf["predicted_cluster"] = pasca
pcadf["Latitude"] = coor["Northing"]
pcadf["Longitude"] = coor["Easting"]
pcadf.to_csv(f"csv {nama}.csv")
# Plot dataset
fig, ax = plt.subplots(figsize=(15, 10))
sns.scatterplot(x="PC1",
y="PC2",
edgecolors="black",
linewidth=0.5,
s=300,
data=pcadf,
hue="predicted_cluster",
palette="plasma")
plt.legend(fontsize="large", loc=1)
ax.axhline(y=0, color='gray', alpha=0.5)
ax.axvline(x=0, color='gray', alpha=0.5)
for i, feature in enumerate(parameter):
plt.arrow(0,
0,
4 * loadings[i, 0],
4 * loadings[i, 1],
color='black',
width=0.01,
head_width=0.1)
plt.text(4.2 * loadings[i, 0],
4.2 * loadings[i, 1],
feature,
color = "red",
fontsize="large")
plt.title(f"{nama}")
plt.show()
fig2, ax = plt.subplots(figsize=(15, 10))
sns.scatterplot(x="PC1",
y="PC3",
edgecolors="black",
linewidth=0.5,
s=300,
data=pcadf,
hue="predicted_cluster",
palette="plasma")
plt.legend(fontsize="large", loc=1)
ax.axhline(y=0, color='gray', alpha=0.5)
ax.axvline(x=0, color='gray', alpha=0.5)
for i, feature in enumerate(parameter):
plt.arrow(0,
0,
4 * loadings[i, 0],
4 * loadings[i, 1],
color='black',
width=0.01,
head_width=0.1)
plt.text(4.2 * loadings[i, 0],
4.2 * loadings[i, 1],
feature,
color = "red",
fontsize="large")
plt.title(f"{nama}")
plt.show()
fig3, ax = plt.subplots(figsize=(15, 10))
sns.scatterplot(x="PC2",
y="PC3",
edgecolors="black",
linewidth=0.5,
s=300,
data=pcadf,
hue="predicted_cluster",
palette="plasma")
plt.legend(fontsize="large", loc=1)
ax.axhline(y=0, color='gray', alpha=0.5)
ax.axvline(x=0, color='gray', alpha=0.5)
for i, feature in enumerate(parameter):
plt.arrow(0,
0,
4 * loadings[i, 0],
4 * loadings[i, 1],
color='black',
width=0.01,
head_width=0.1)
plt.text(4.2 * loadings[i, 0],
4.2 * loadings[i, 1],
feature,
color = "red",
fontsize="large")
plt.title(f"{nama}")
plt.show()
kmc("stream sediment sampling", streamn, streamm, loadingsss, data_pca_sss, 4, costream)
kmc("soil sampling", soiln, soilm, loadingss, data_pca_ss, 5, cosoil)
1
silhouette score KMC: 0.5955732674747102
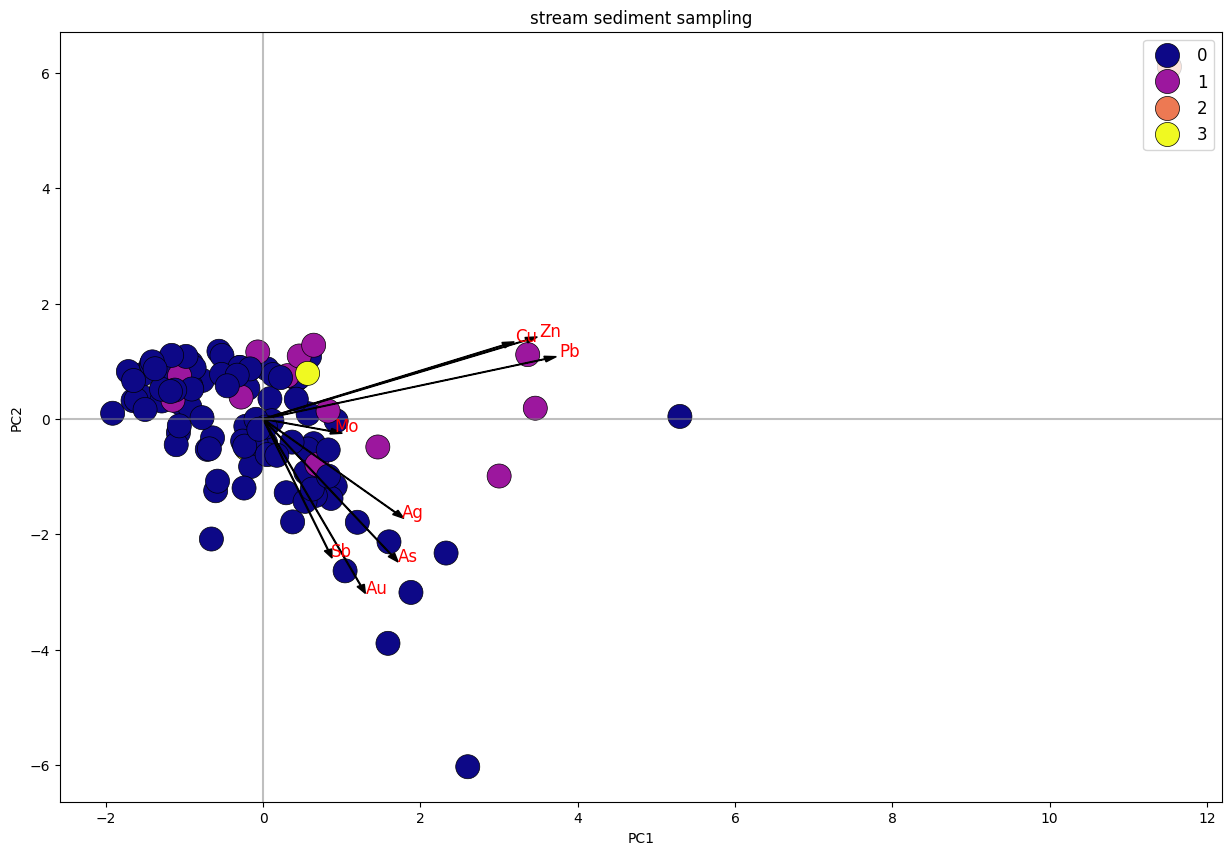Biplot K-Means Clustering PC1 Vs. PC2 Stream Sediment Sampling.
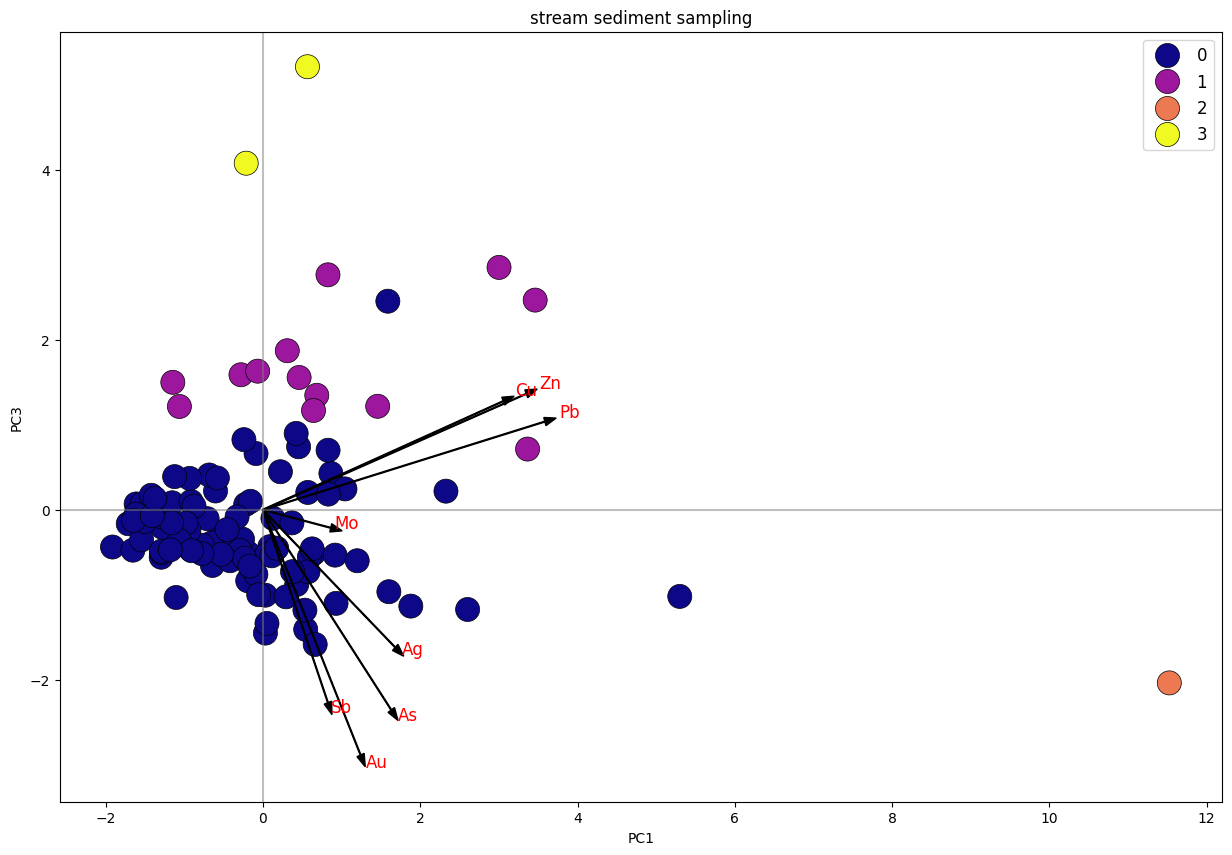Biplot K-Means Clustering PC1 Vs. PC3 Stream Sediment Sampling.
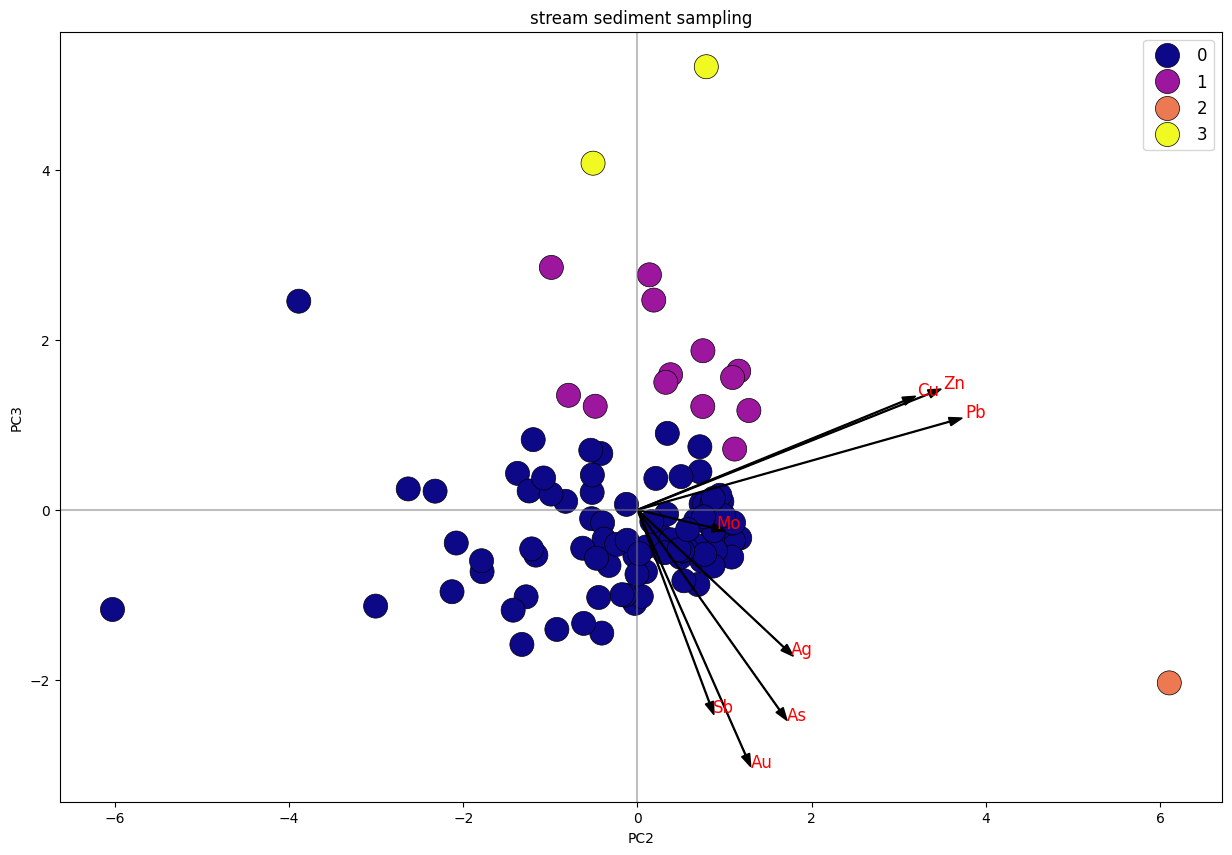_Biplot K-Means Clustering PC2 Vs. PC3
1
silhouette score KMC: 0.7876141221589223
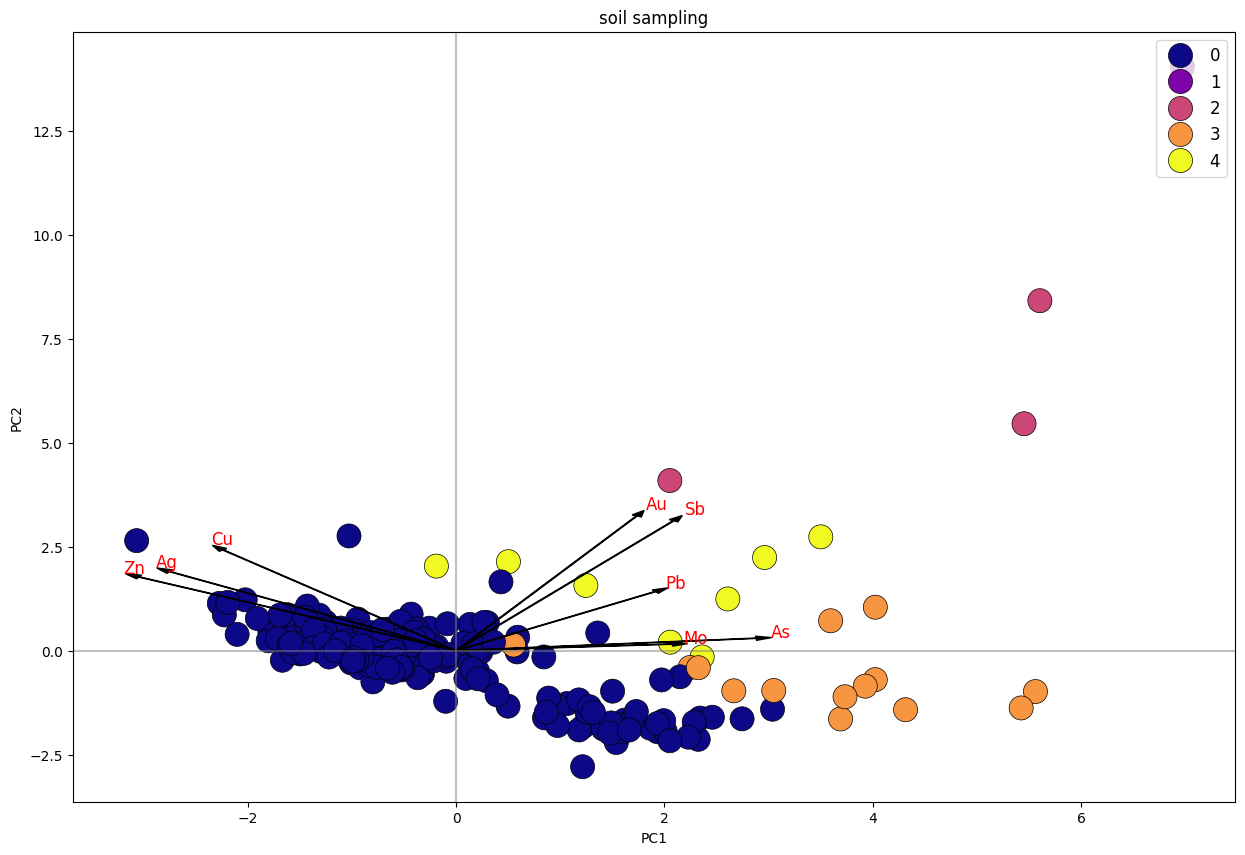Biplot K-Means Clustering PC1 Vs. PC2 Stream Sediment Sampling.
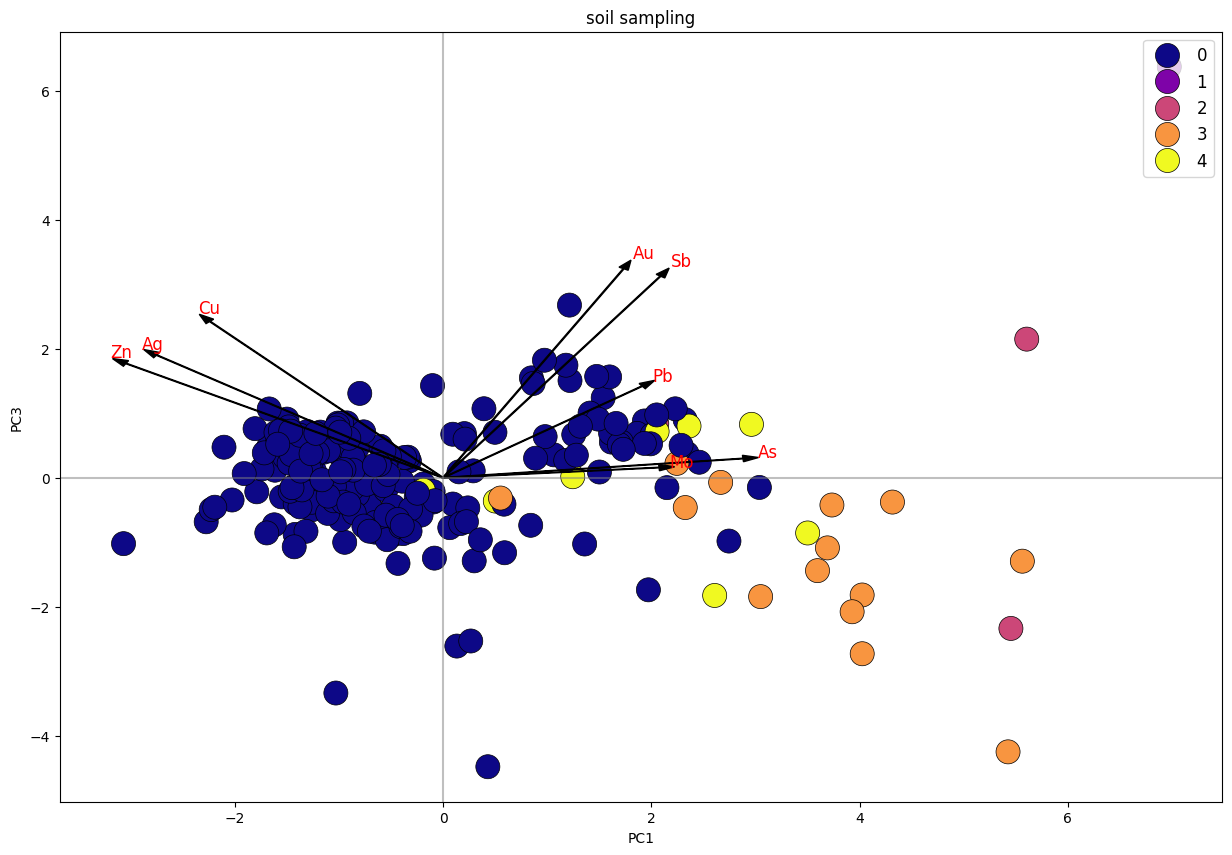Biplot K-Means Clustering PC1 Vs. PC3 Stream Sediment Sampling.
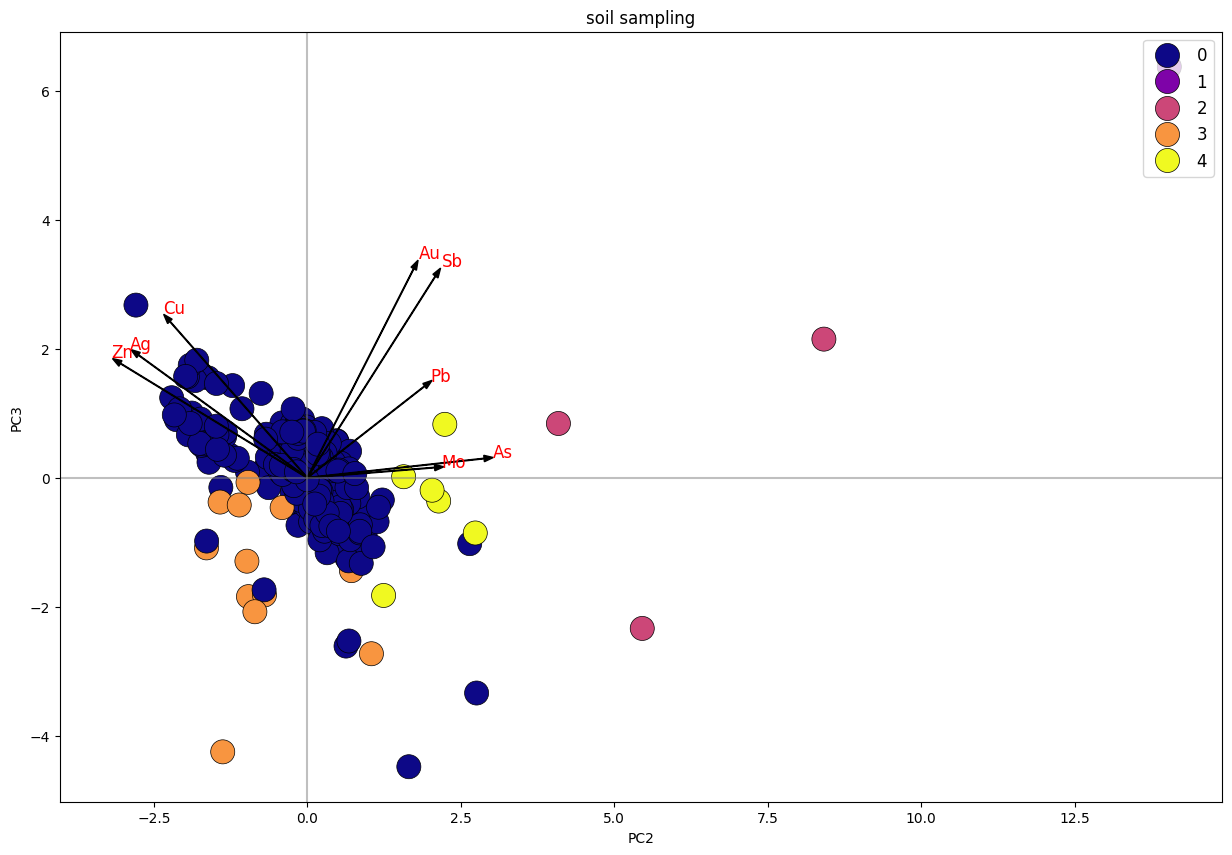Biplot K-Means Clustering PC2 Vs. PC3
Dari plot stream sediment sampling, dapat diketahui bahwa data terbagi menjadi 4 klaster, di mana klaster 1 dan 3 memiliki trend searah dengan unsur Cu, Pb, Zn. sedangkan klaster 1 tersebar merata mengikuti trend unsur Cu-Pb-Zn dan trend Au-As-Ag-Sb. Klaster 2 merupakan anomali.
Pada plot soil sampling, dapat diketahui klaster 0 memiliki 2 arah trend, yakni yang positif dengan unsur Cu-Ag-Zn dan Au-Sb-Pb. sedangkan klaster lainnya positif dengan unsur Au-Sb-Pb.
2. Peta Anomali
A. Peta Anomali Data Stream Sediment Sampling
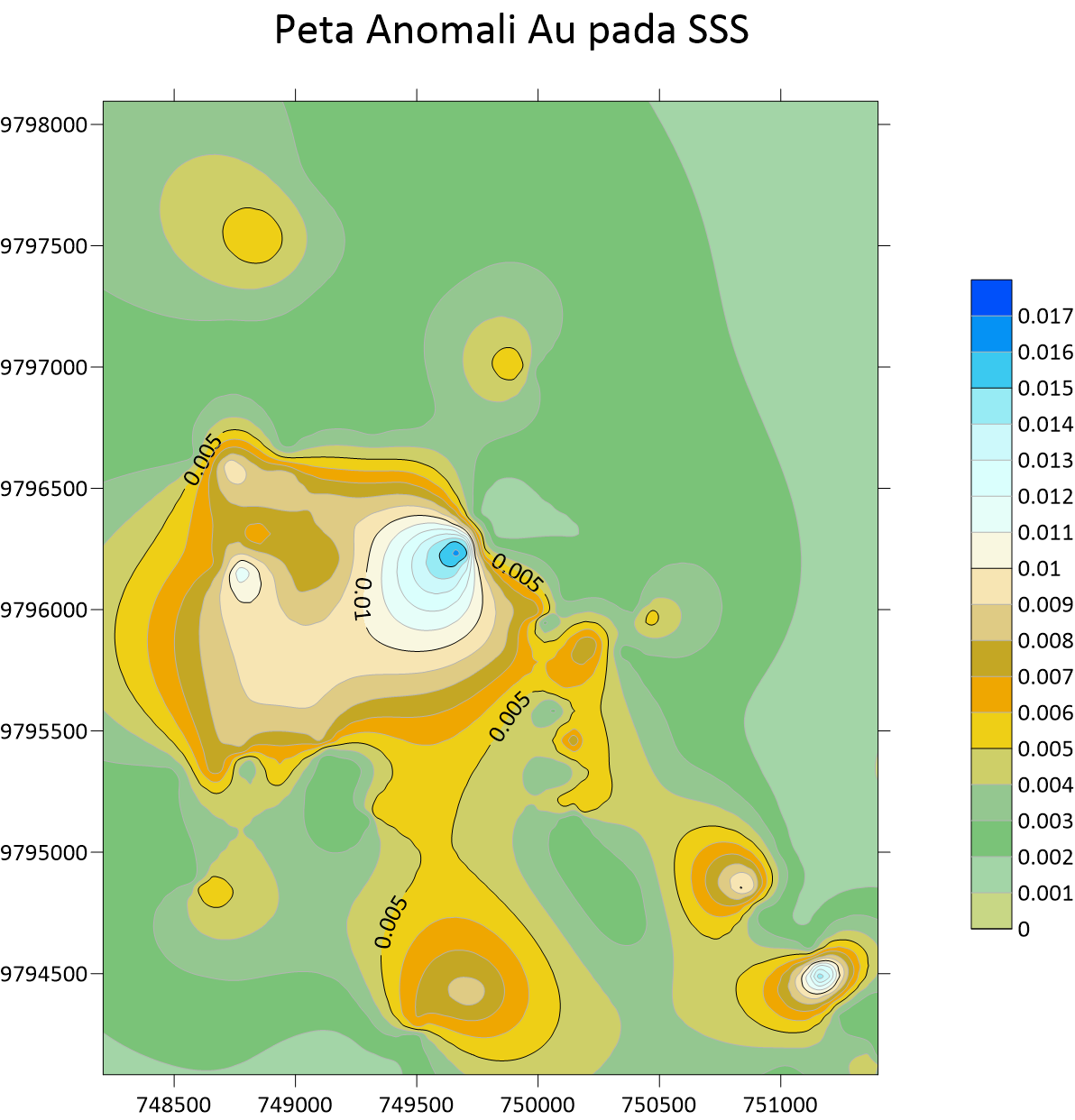Peta Anomali Au Stream Sedimen 
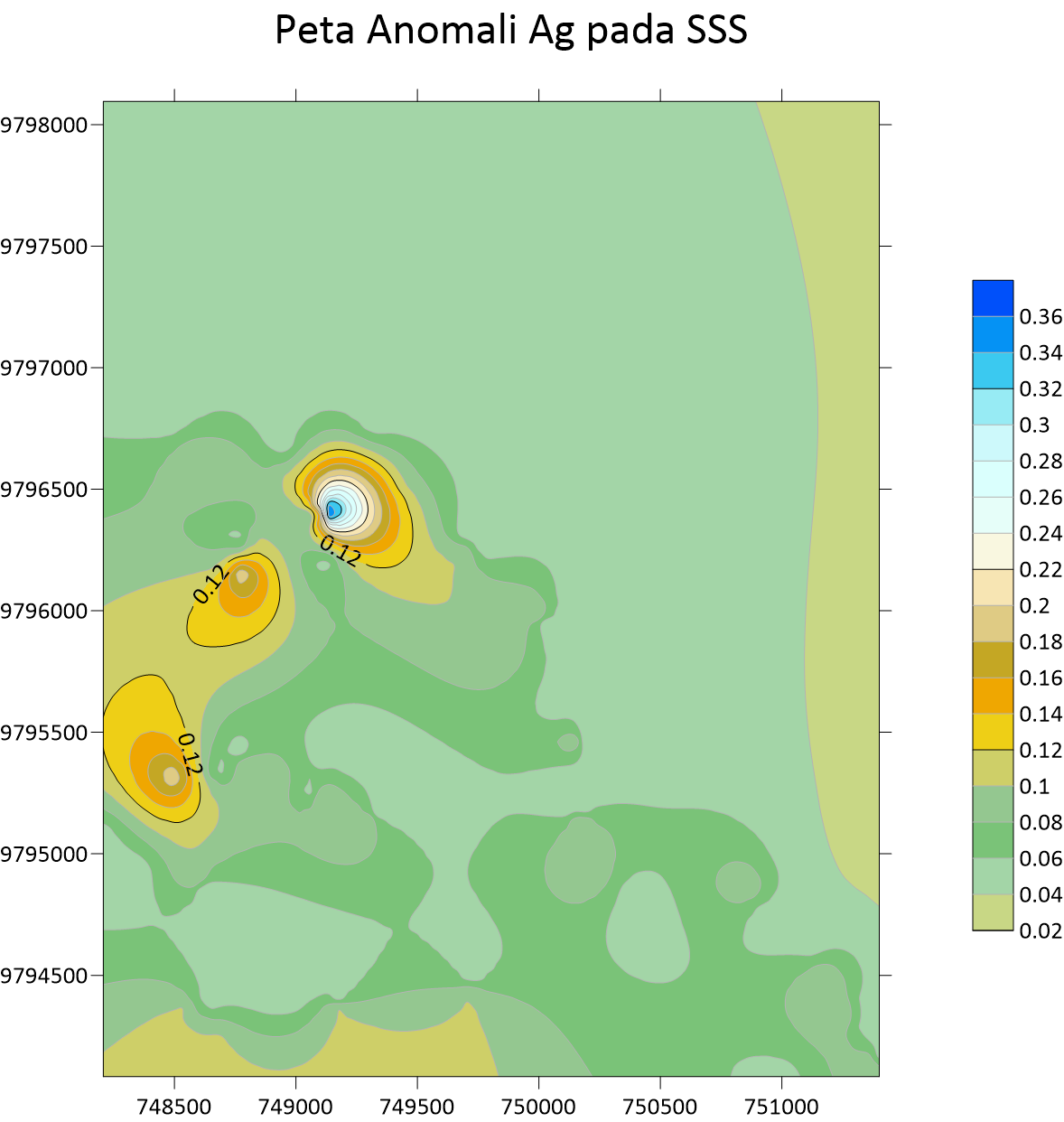Peta Anomali Ag Stream Sedimen Sampling 
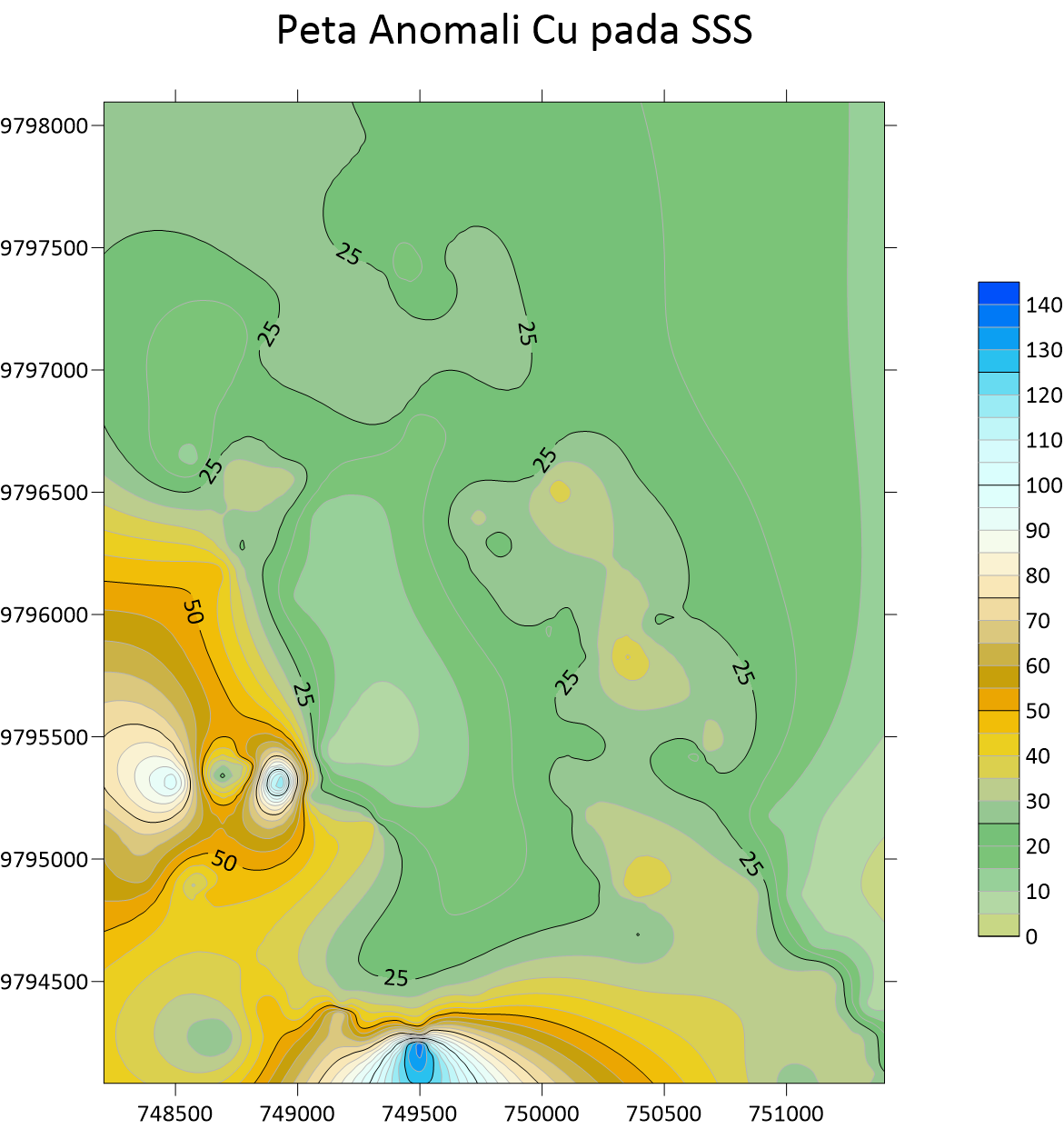Peta Anomali Cu Stream Sedimen Sampling 
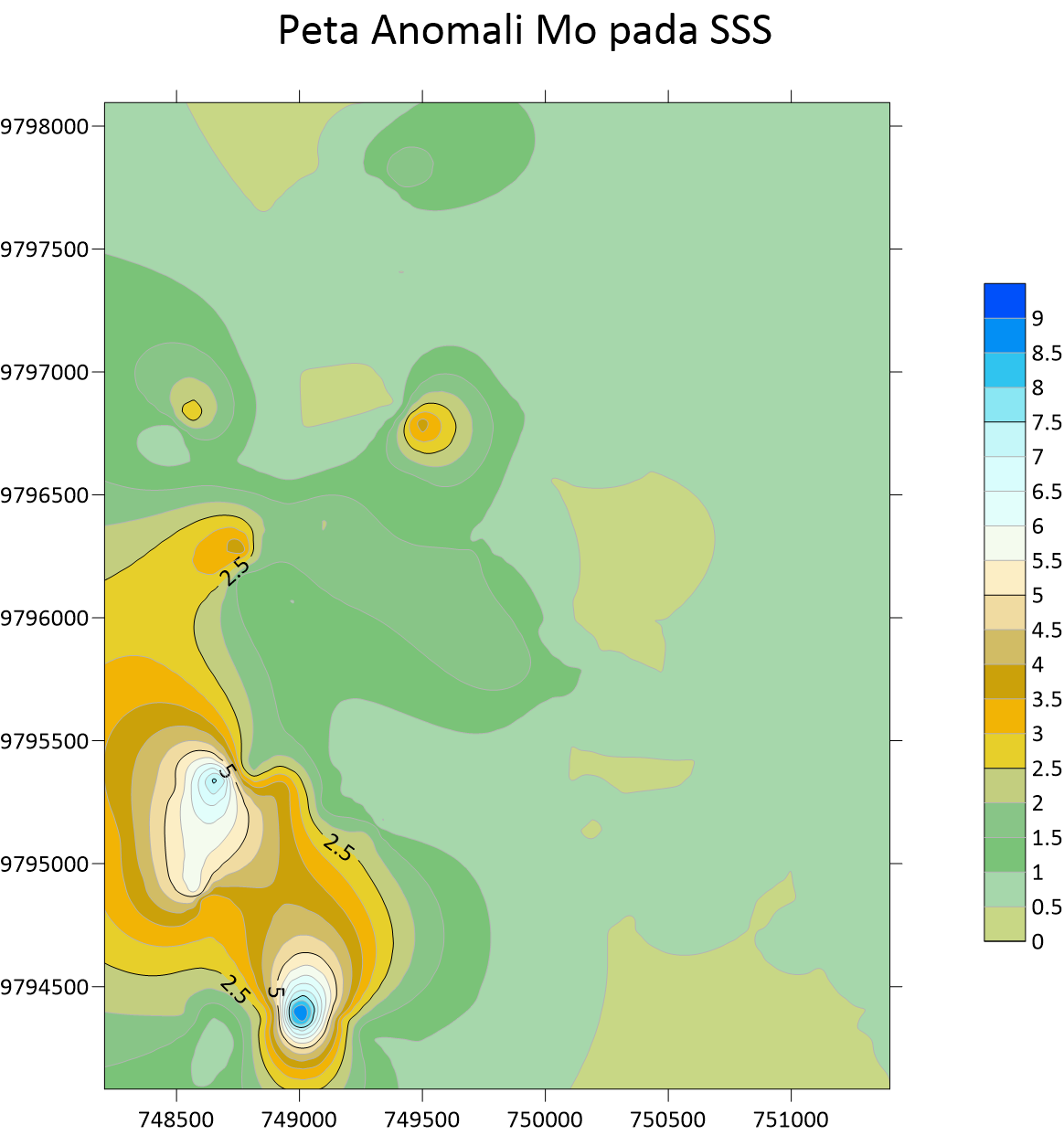Peta Anomali Mo Stream Sedimen Sampling 
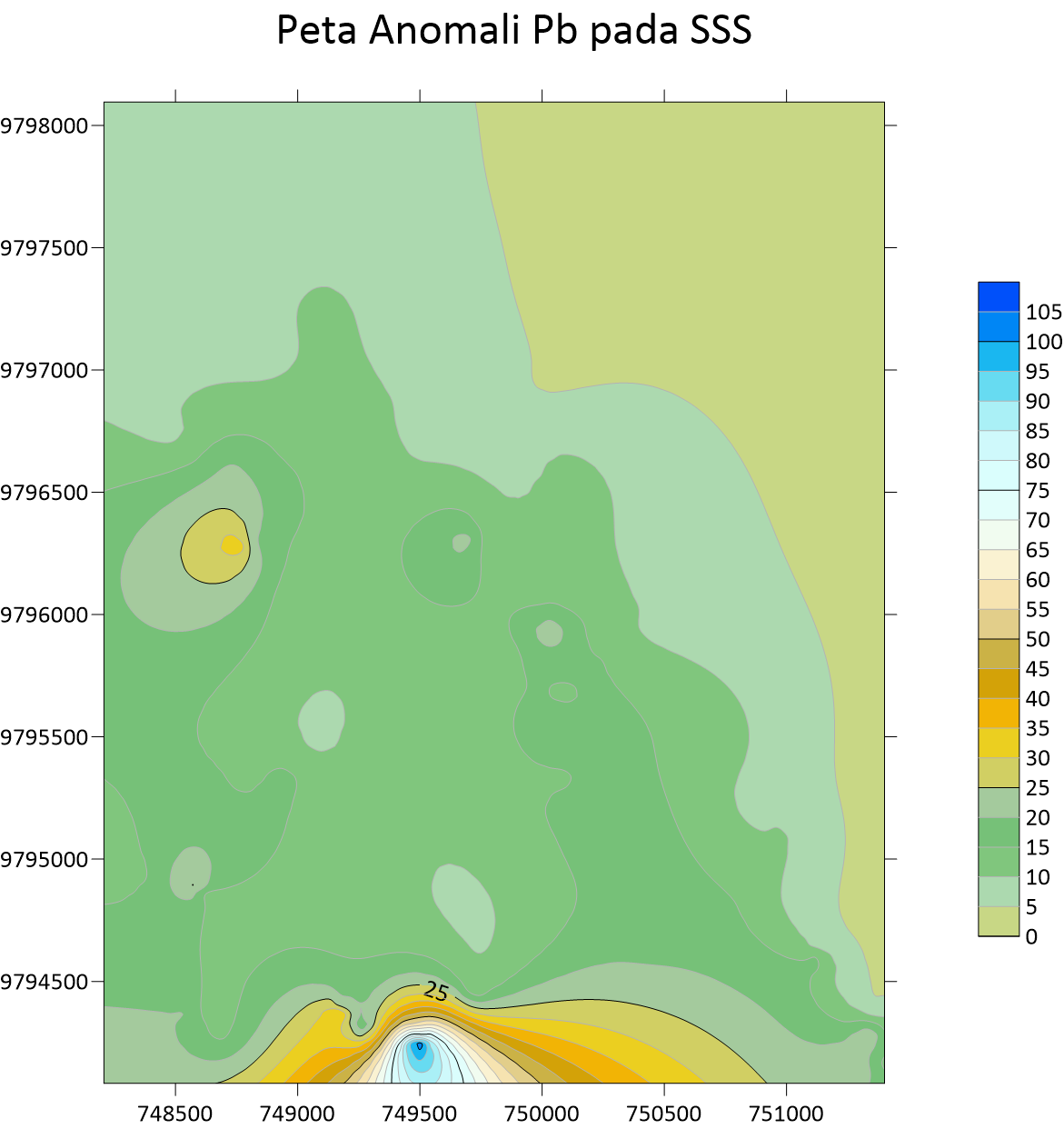Peta Anomali Pb Stream Sedimen Sampling 
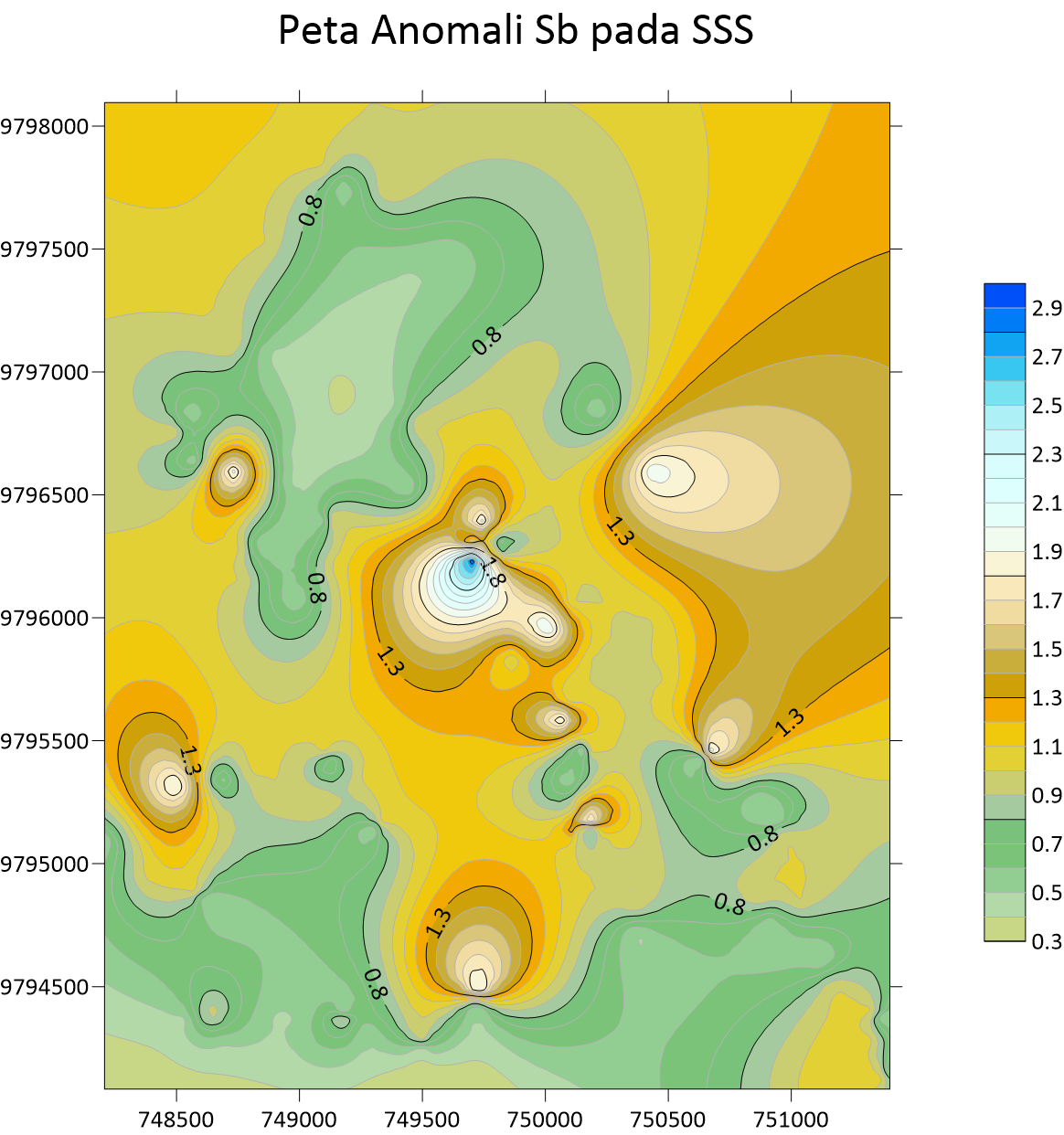Peta Anomali Sb Stream Sedimen Sampling 
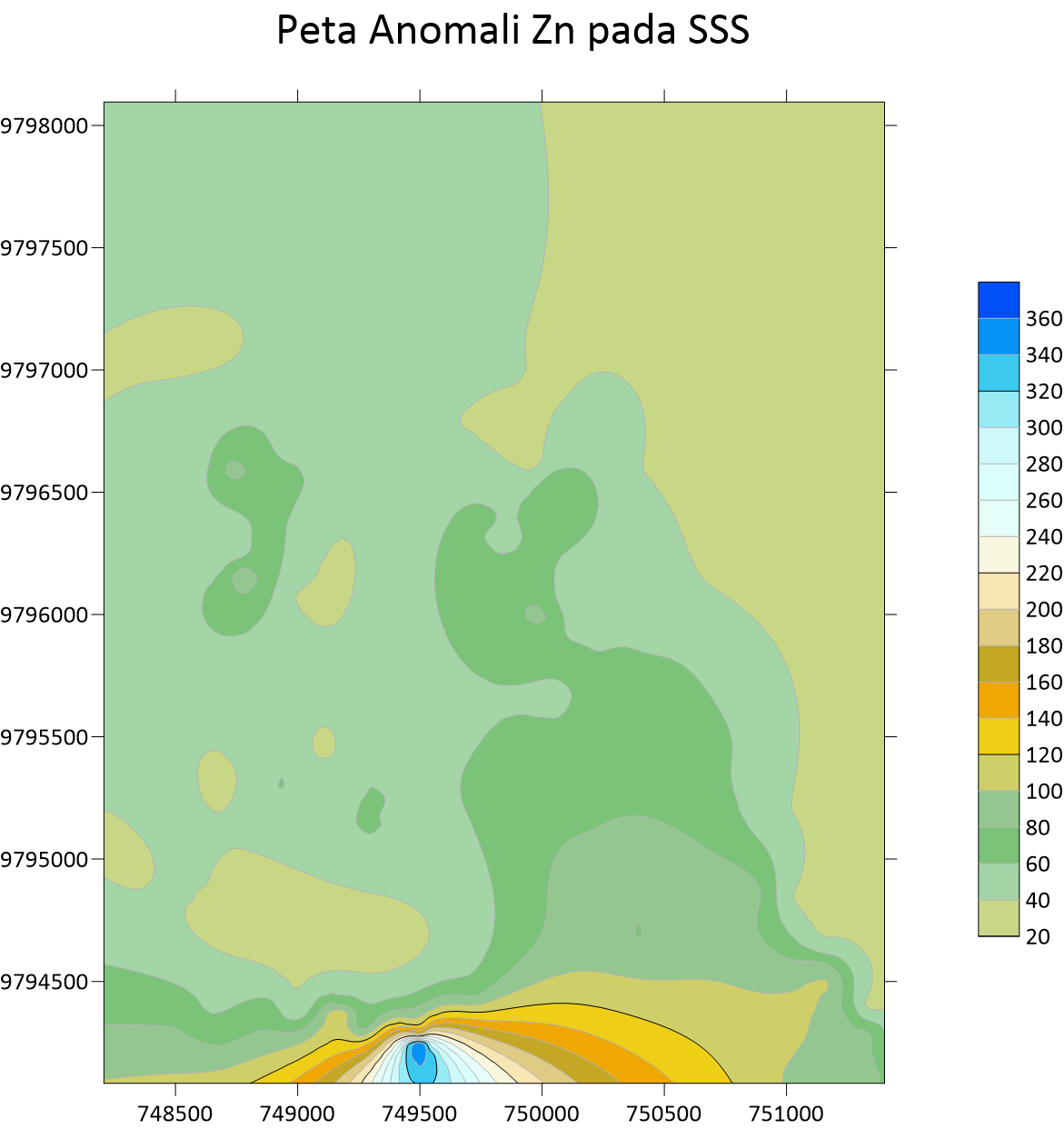Peta Anomali Zn Stream Sedimen Sampling
B. Peta Anomali Data Soil Sampling
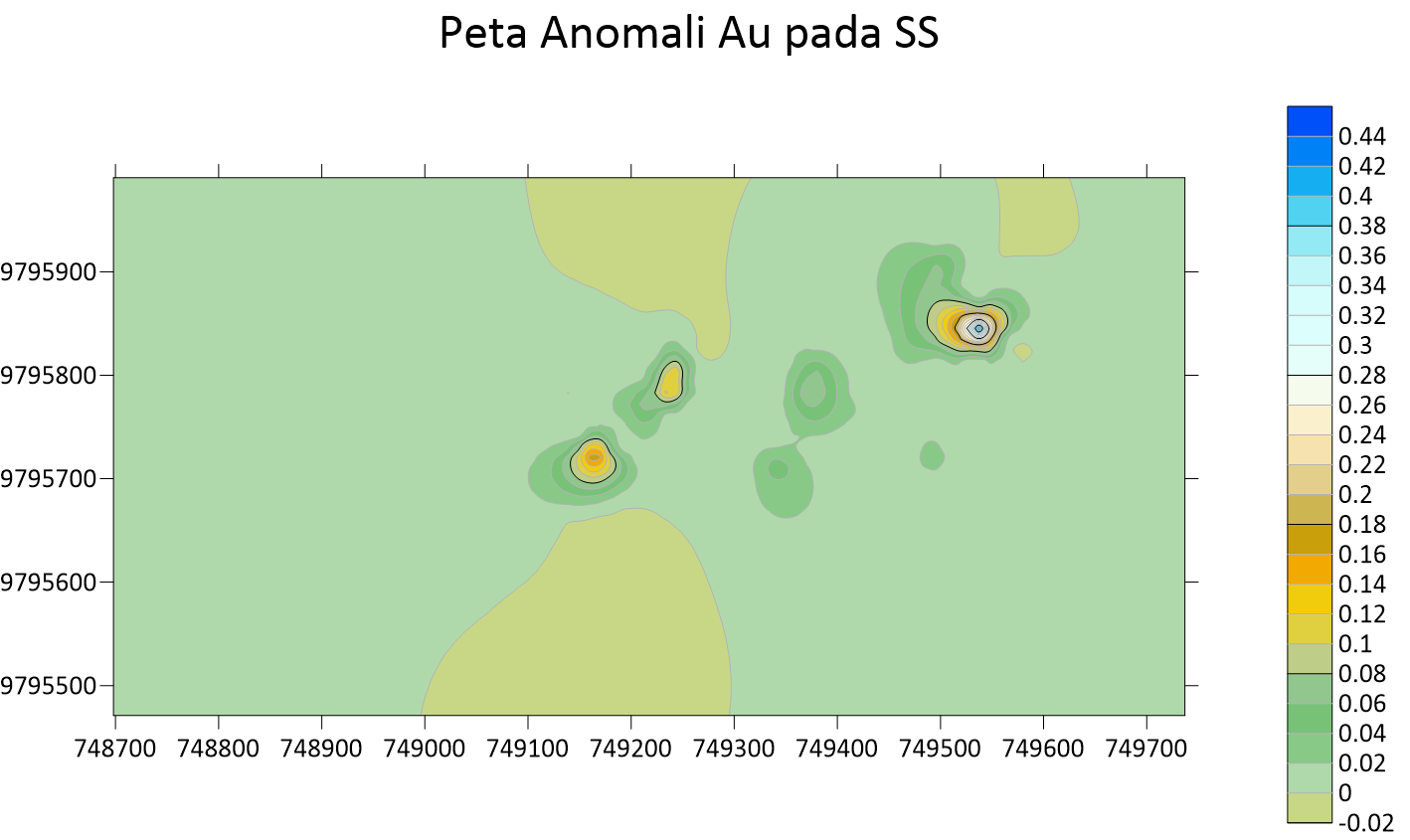Peta Anomali Au Soil Sampling 
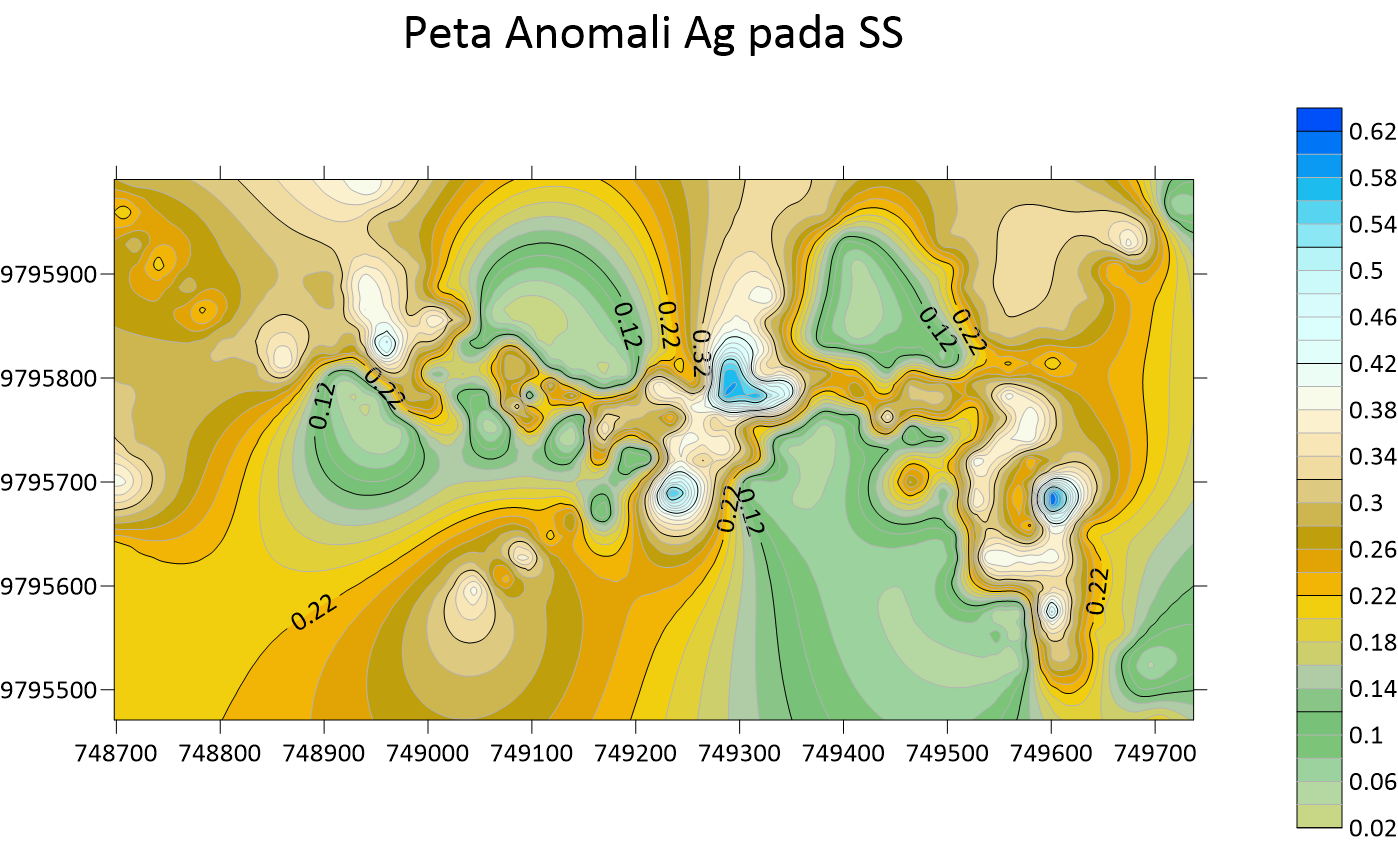Peta Anomali Ag Soil Sampling 
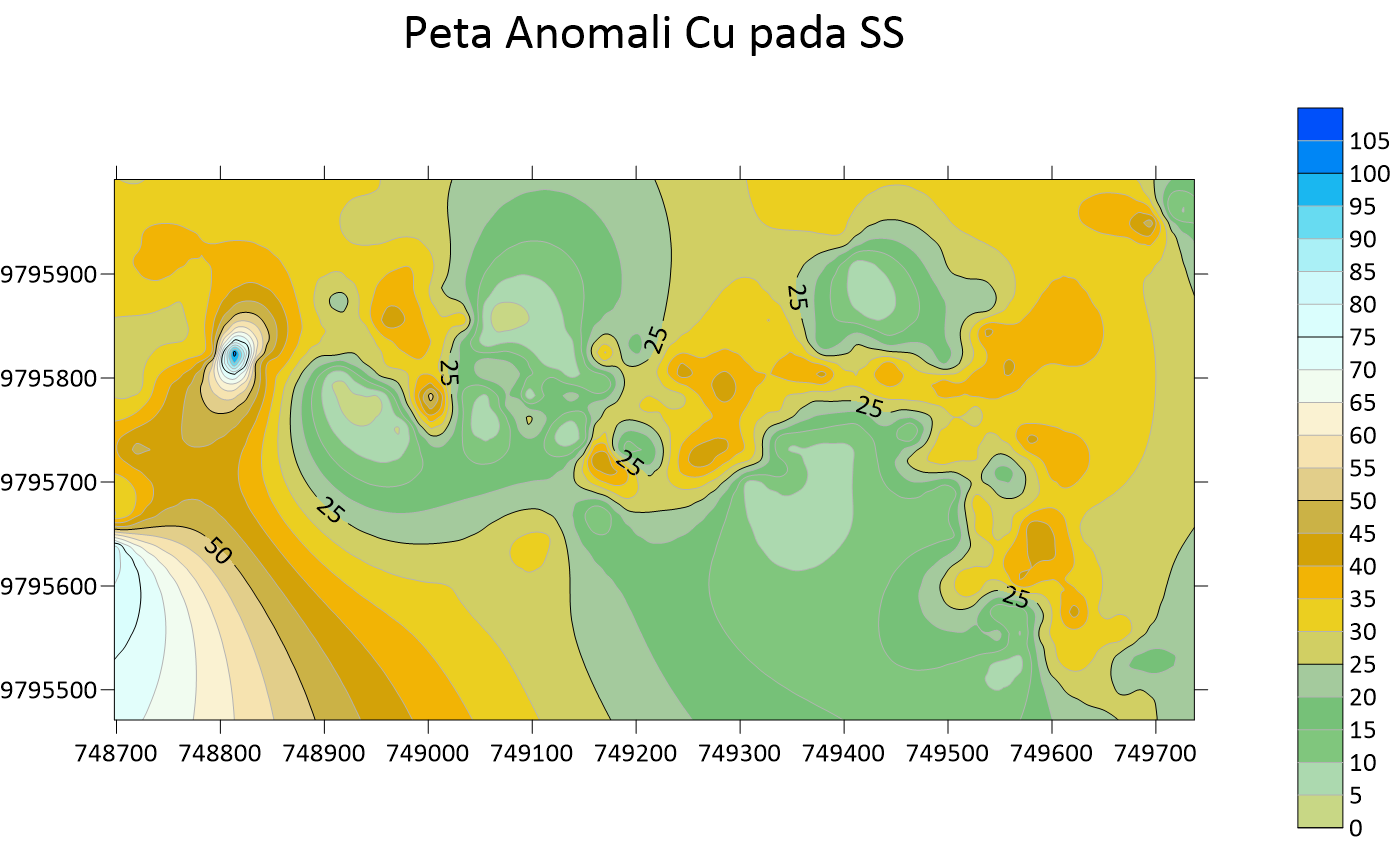Peta Anomali Cu Soil Sampling 
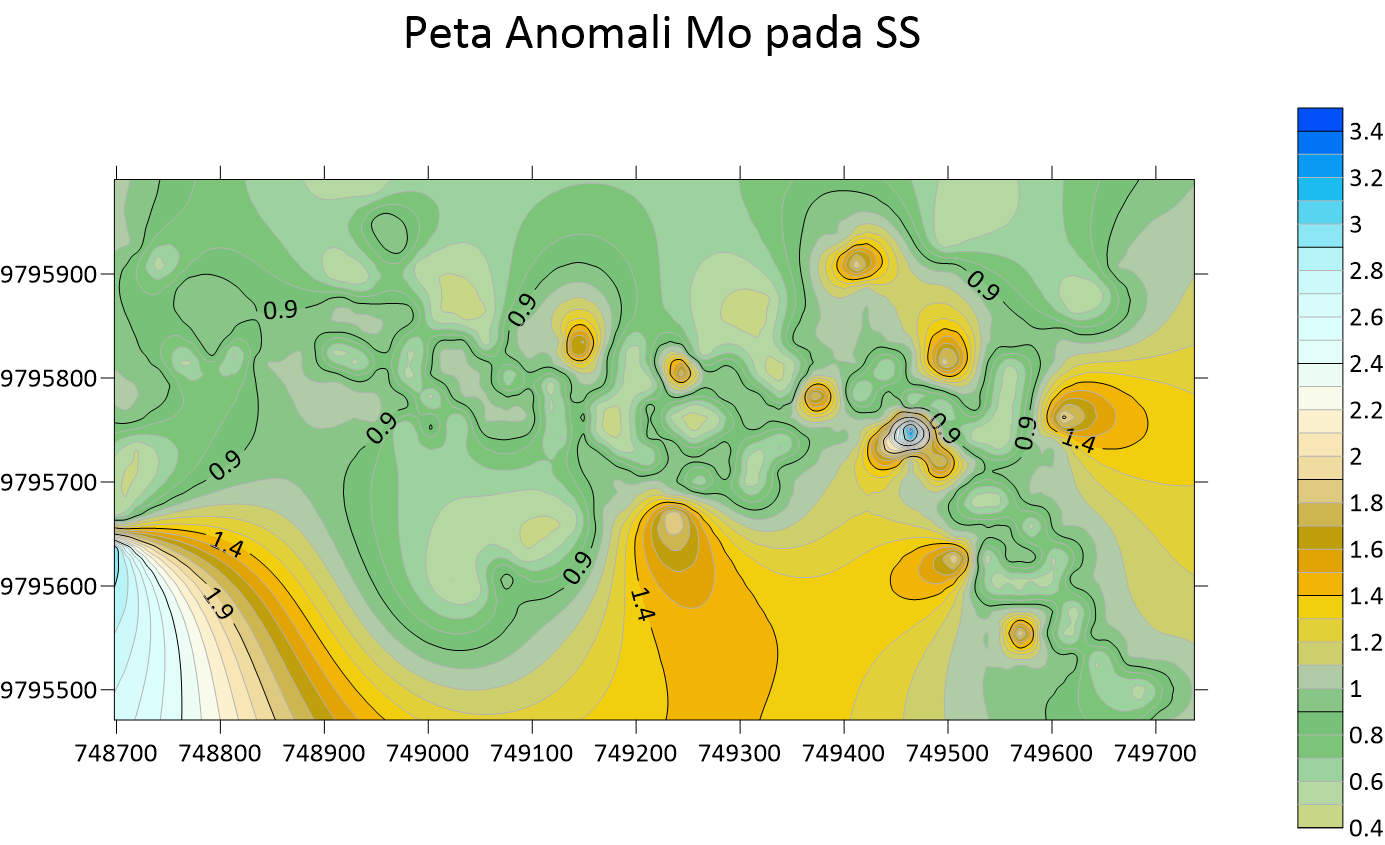Peta Anomali Mo Soil Sampling 
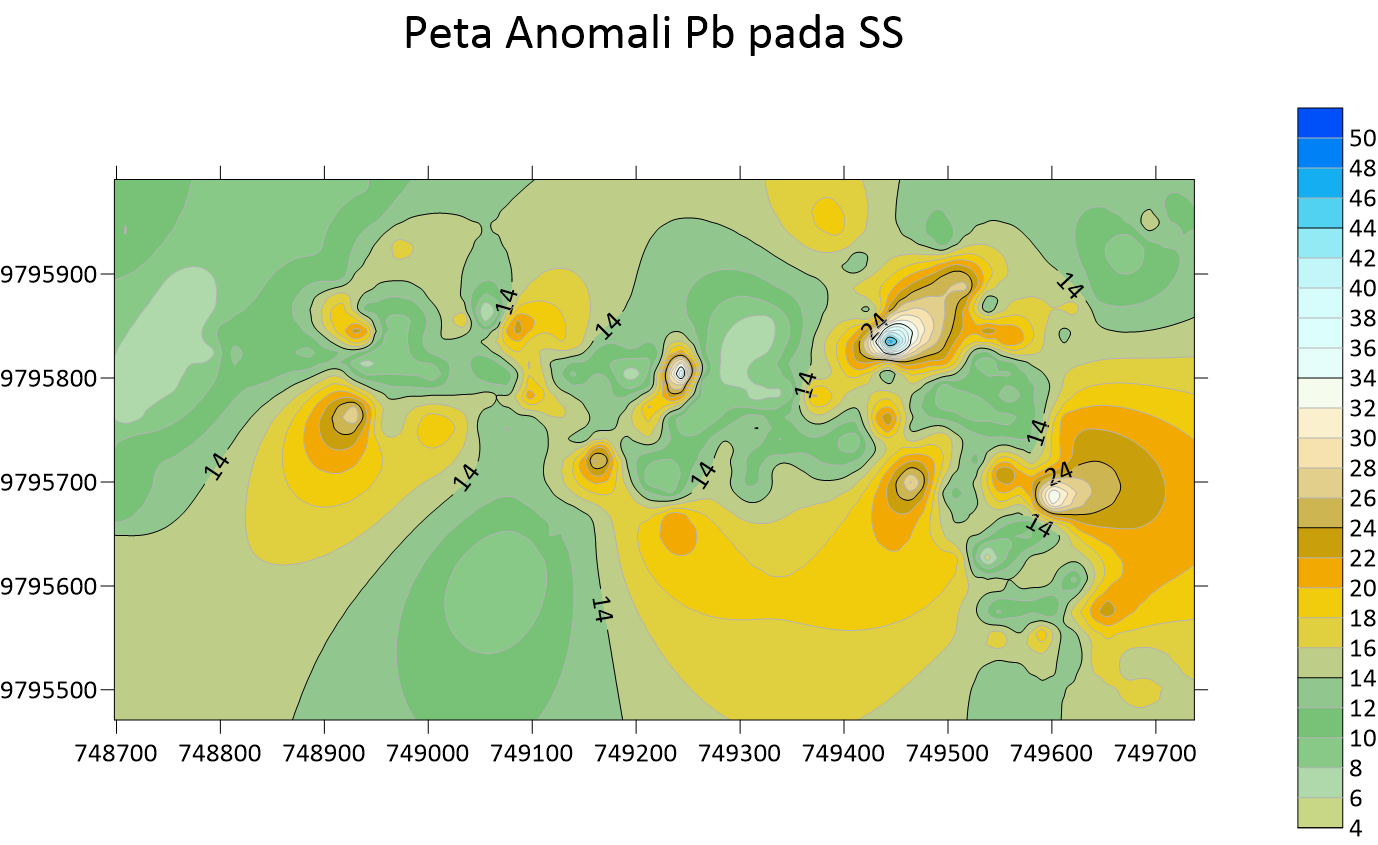Peta Anomali Pb Soil Sampling 
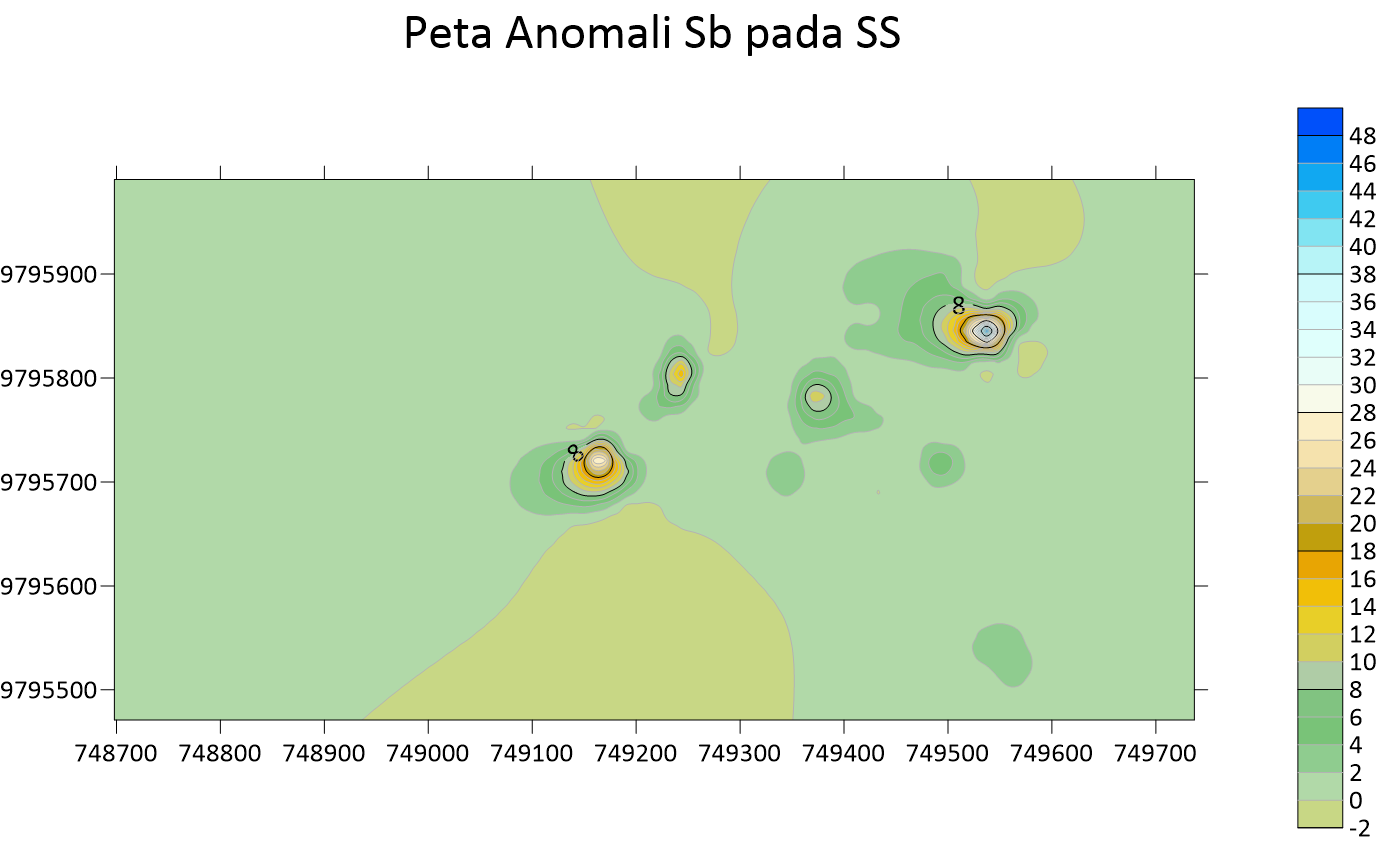Peta Anomali Sb Soil Sampling 
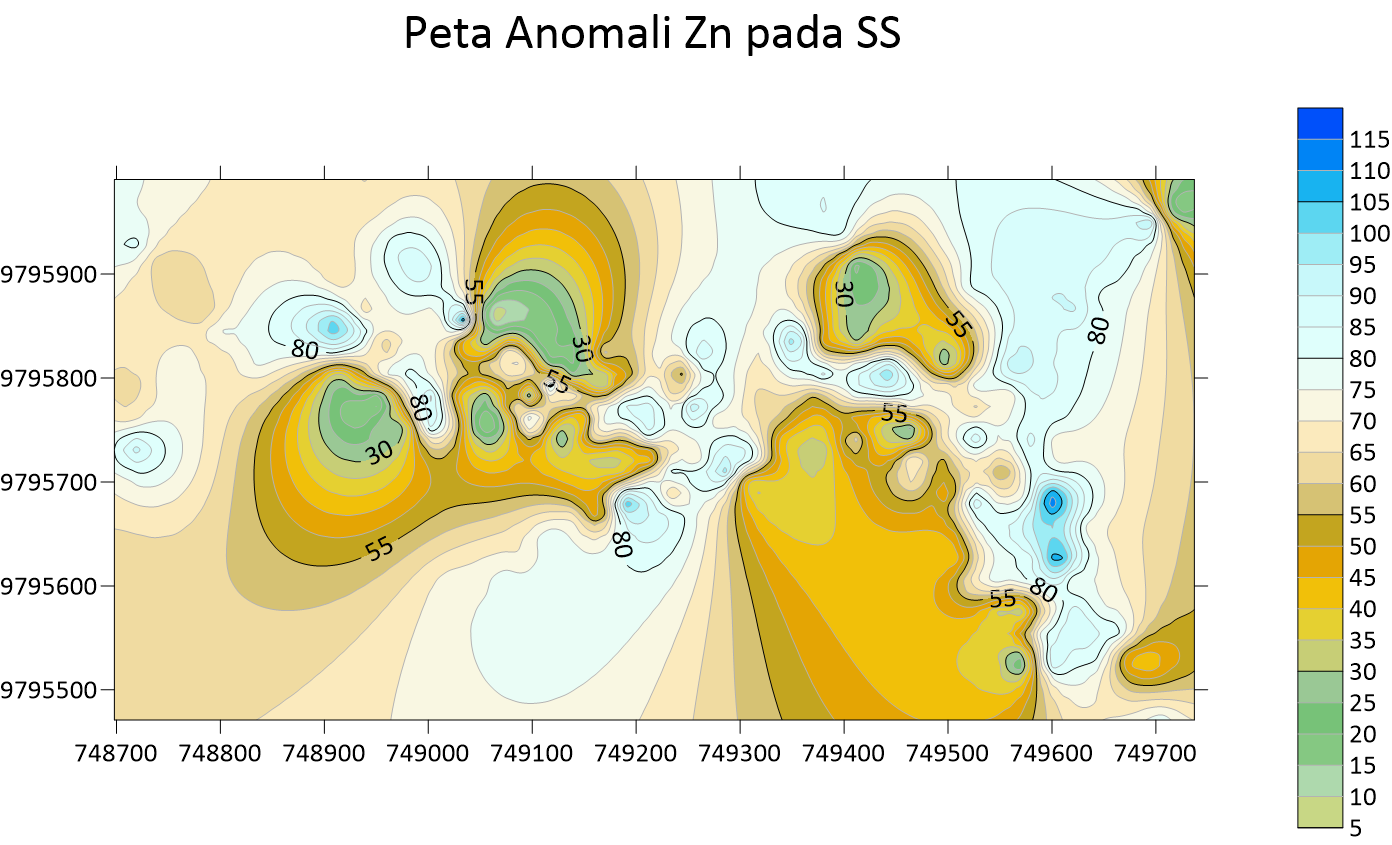Peta Anomali Zn Soil Sampling
This post is licensed under CC BY 4.0 by the author.